Необходимо разработать конструкцию и рассчитать основные параметры механизма датчика скорости летательного аппарата (ДС).
1.2 Разработка функциональной схемы механизма.
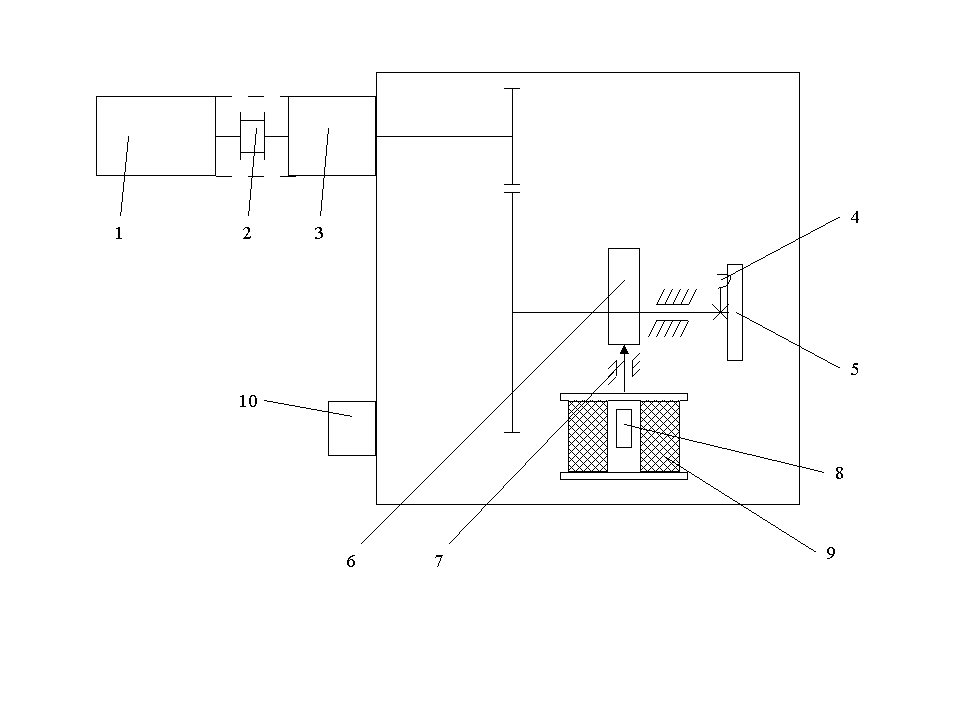
Блок датчика динамического давления (ДС) предназначен для определения скорости летательного аппарата. Механизм отработки сигнала от датчика (рис. 1) состоит из : электродвигателя 1, соединительной муфты 2, редуктора 3, щетки 4, потенциометра 5, кулачка 6, индуктивного датчика 9, толкателя 7 и сердечника 8, штепсельного разъема 10.
При вращении кулачка 6 толкатель 7 перемещает внутри катушки 9 сердечник 8, тем самым, изменяя ее индуктивность. Потенциометр, индуктивный датчик и кулачковый механизм укрепляются в изолированной от редуктора части корпуса. Угол поворота выходного вала, на котором укреплены реохорд и кулачок, не превышает 70° .

Рис.1
По формуле находят мощность
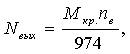 (1)
(1)
где
![]()
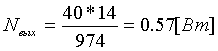
Зная мощность
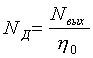 ,
,
где h
0 –общий КПД механизма.Так как определение номинальной мощности электродвигателя и выбор его проводится до составления кинематической схемы, то в первом приближении общий КПД можно принять h
0 =0.6.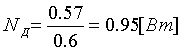
Результаты выбора двигателя Таблица 1
|
|
|
h 0 , % |
|
Вт |
Марка двигателя |
|
40 |
14 |
60 |
0.57 |
0.95 |
Г-205 |
Параметры двигателя представлены в таблице 2 , внешний вид изображен на рисунке 2.
Характеристики двигателя Г-205 Таблица 2
|
Мощ-ность Вт |
Часто-та Враще-ния, Об/мин |
Номи-наль-ный Момент Н× см |
Момент Инерцииякоря кг× см 2 |
Пуско-вой Момент Н× см |
Габариты |
|||
|
D, мм |
L, мм |
D, мм |
l, мм |
|||||
|
1 |
3000 |
0,33 |
0,057 |
1,35 |
58 |
79 |
4 |
5 |
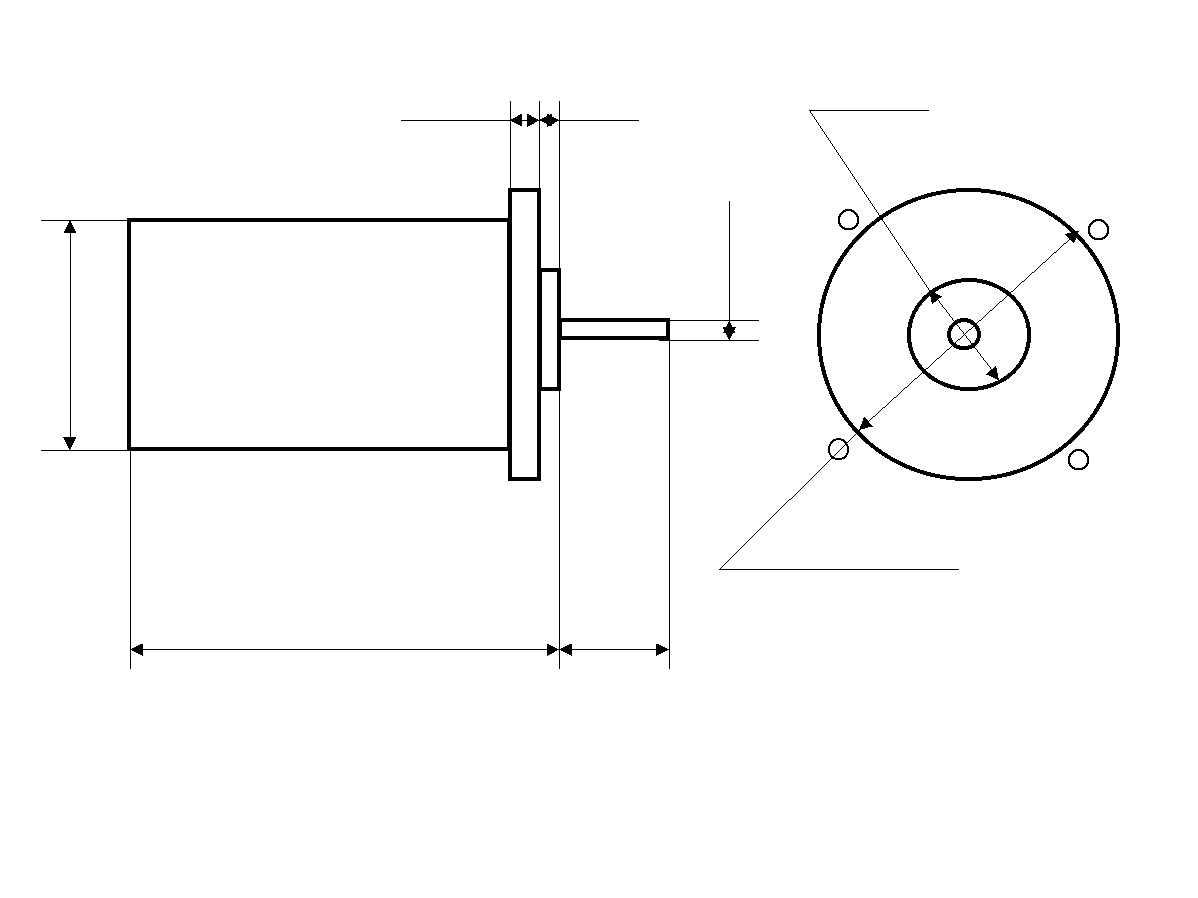
Рис. 2
Для понижения числа оборотов двигателя выбран редуктор с рядным соединением прямозубых цилиндрических зубчатых колес.
Передаточное отношение редуктора
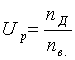 , (3)
, (3)
где
![]() -
-
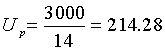
Передаточное отношение редуктора можно представить как произведени передаточных отношений ступеней редуктора согласно формуле
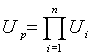 , (4)
, (4)
где
Представим передаточное отношение в таком виде по формуле (4). Получим:
![]() .
.
Подбор чисел зубьев проводится согласно формуле
![]() , (5)
, (5)
где
![]()
![]()
Рассчитаем число зубьев для колеса второй ступени
![]()
С использованием формул (4) и (5) были подобраны передаточные отношения пар зубчатых колес и числа зубьев. Эти величины представлены в таблице 3.
Передаточные отношения ступеней и числа зубьев Таблица 3
|
Передаточное отношение редуктора |
Передаточное отношение ступеней |
Обозначение шестерни, колеса |
Число зубьев шестерни, колеса |
||
|
Расчетное |
Действительное |
||||
|
Расчетное |
Действительное |
||||
|
214.28 |
215 |
2.14 |
2.15 |
|
20 |
|
|
43 |
||||
|
4 |
4 |
|
18 |
||
|
|
72 |
||||
|
5 |
5 |
|
18 |
||
|
|
90 |
||||
|
5 |
5 |
|
18 |
||
|
|
90 |
||||
Кинематическая схема редуктора представлена на рисунке 3.
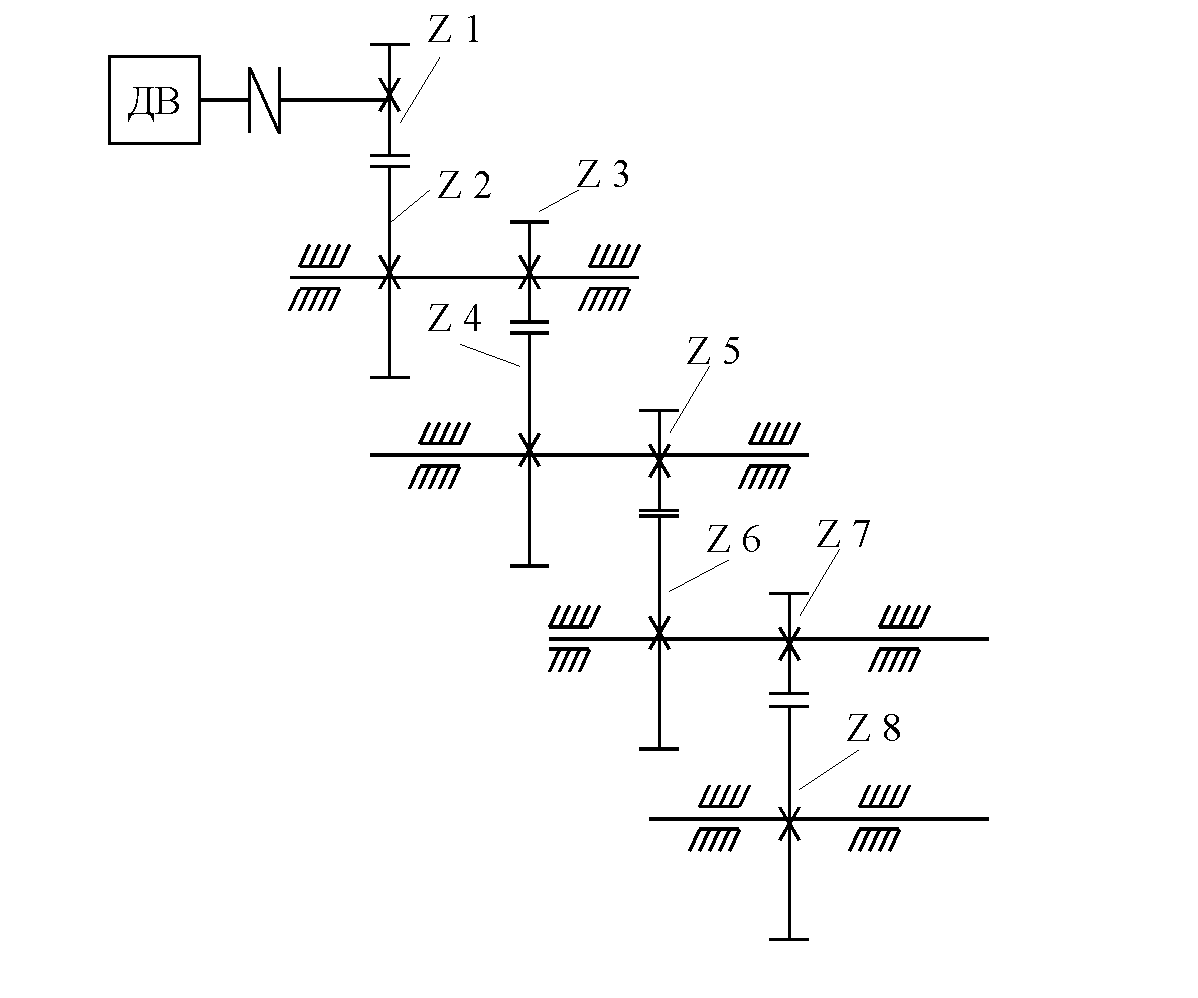
Рис. 3
Так как полученное передаточное отношение редуктора отличается от требуемого, при его работе возникает ошибка
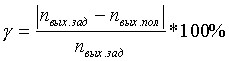 , (6)
, (6)
где
![]()
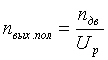 ,
, ![]() (7)
(7)
где
![]()
Рассчитаем
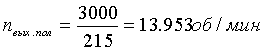 ,
, 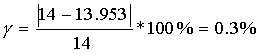 .
.
Результаты расчета ошибки передачи Таблица 4
|
|
|
|
|
|
|
3000 |
215 |
14 |
13.953 |
0.3% |
Полученное значение ошибки передачи укладывается в допустимые пределы.
При подборе двигателя использовалось произвольное значение КПД редуктора h
0 =60%. Теперь необходимо рассчитать его действительное значение![]() , (8)
, (8)
где
![]()
![]()
![]() -
-
Рассчитаем КПД редуктора. Получим.
![]() .
.
Результат расчета КПД редуктора Таблица 5
|
|
|
|
|
|
|
0.98 |
0.97 |
0.99 |
0.98 |
0.769 |

2.5
Расчет крутящих моментов
где
Исходя из того что момент на последнем валу нам известен (момент на выходном валу) –можно по формуле (9) рассчитать моменты на стальных валах.
Результаты этих расчетов приведены в табл.6
|
|
|
|
|
|
|
0.2 |
0.423 |
1.66 |
8.16 |
40 |
Максимальный момент
2.51
Расчет размеров зубчатых колесРасчет модуля зубчатого колеса
Выберем для зубчатой передачи следующие материалы:
Модуль для цилиндрического прямозубого колеса определяется по формуле:
 (10)
(10)
2) при расчете на изгиб:
 (11)
(11)
Для расчета модуля рассчитаем необходимые параметры.
Коэффициент, учитывающий разнородность материалов колеса и шестерни:
 (12)
(12)
Исходя из выбранных материалов, ЕШ
=2,15× 107н/см2 и ЕК=9,3× 106н/см2: ![]()
Найдем расчетный крутящий момент на валу колеса:
![]() , (13)
, (13)
Примем следующие коэффициенты
![]()
Вычислим значение модуля при расчете на контактное напряжение по формуле (1
0):U=5
, коэффициент ширины зуба примем y =8. Для материала колеса допустимое контактное напряжение на сдвиг равно: [t к]к=10000 Н/см2.  мм
мм
Вычислим значение модуля при расчете на изгиб:
Число зубьев шестерни и колеса: ZШ
=Z7=18, ZК=Z8=90. Эквивалентное число зубьев шестерни и колеса для прямозубой цилиндрической передачи: ZЭКВ.Ш =18, ZЭКВ.К=90. Этим значениям соответствуют следующие коэффициенты формы зуба: yш=0,098, yк=0,1405.Определим слабое звено. Для материала колеса допустимое напряжение на изгиб [s и
]к=11000 н/см2, для материала шестерни [s и]ш=19000 н/см2. ![]()
![]()
Слабым звеном является колесо, поэтому в формулу (
11) подставляем его параметры.Определим расчетное значение крутящего момента на валу шестерни:

Исходя из проведенных расчетов, принимаем
m=0,6мм.Ширина
b для всех колес одинакова и равна: ![]() (14)
(14)
Диаметры делительной окружности, окружности выступов и окружности впадин вычисляются по следующим формулам:
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
Рассчитаем диаметр делительной окружности, окружности выступов и окружности впадин для колеса
![]() ,
,
![]()
![]()
Размеры колес сведем в таблицу 7.
Таблица 7.
Размеры зубчатых колес
|
Колесо |
Число зубьев |
Размеры в мм |
|||
|
D |
da |
Df |
b |
||
|
Z1 |
20 |
12 |
13,2 |
10,5 |
5,8 |
|
Z2 |
43 |
25,8 |
27 |
24,3 |
4,8 |
|
Z3 |
18 |
10,8 |
12 |
9,3 |
5,8 |
|
Z4 |
72 |
43,2 |
43,4 |
41,7 |
4,8 |
|
Z5 |
18 |
10,8 |
12 |
9,3 |
5,8 |
|
Z6 |
90 |
54 |
55,2 |
52,5 |
4,8 |
|
Z7 |
18 |
10,8 |
12 |
9,3 |
5,8 |
|
Z8 |
90 |
54 |
55,2 |
52,5 |
4,8 |
2.6
Расчет валовРасчет выполняется для последнего и предпоследнего вала
2.61
Расчет реакций в опорах выходного вала(l1=0.05 l2=0.015 l3=0.02)
Рассмотрим плоскость
XOZ (Рис. 4)
Рис. 4
Кроме распорных и окружных сил в зацеплениях на выходной вал действуют радиальная
Pko ,Н и окружная Pkr ,Н силы со стороны кулачка. Профиль кулачка представлен на рисунке 5. Силы определяются по формулам (18), (20) при их определении учитывается то , что плоскости зацеплений на валу и плоскость контакта кулачка с толкателем находятся по углом 45 градусов.
Рис. 5
Найдем действующие на вал силы:

Вычислим окружные силы


C
илы Px и Pkx рассчитываются по формулам![]() (19)
(19)
![]()
Вычислим силы
Px и Pkx![]()
![]()
![]()
![]()
![]()
Решая данную систему уравнений найдем реакции в опорах:
![]()
Рассмотрим плоскость YOZ (Рис.6)
Рис. 6
![]()
Выразим Рkу используя формулу (18)
![]()
Из формулы (21) следует ,что :
![]()
![]()
Решая данную систему уравнений найдем реакции в опорах:
![]()
2.62
Расчет реакций в опорах предвыходного вала(l1=0.035 l2=0.015 l3=0.02)Рассмотрим плоскость
XOZ
Рис. 7
Для наглядности расчетов на рисунке 8 показано взаимное расположение зацеплений на предвыходном валу.

Рис. 8
Получим выражения для
Px и Prx пользуясь формулой (18)![]()
![]()
![]()
![]()
Из формулы (21) следует ,что :
Решая данную систему уравнений найдем реакции в опорах:![]()
![]()
![]()
Рассмотрим плоскость
YOZ
Рис. 9
Получим выражения для
Py и Pry пользуясь формулой (18)![]()
![]()
Вычислим значения этих величин
![]()
![]()
![]()
![]()
Составим таблицу изгибающих моментов на валах
Таблица 8
|
Изгибающие моменты на входном валу |
|
|
XOZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
YOZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Изгибающие моменты на предвыходном валу |
|
|
XOZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
YOZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
2.63
Эпюры для выходного вала
Рис. 10
YOZ
Рис. 11
2.64
Эпюры для предвыходного валаXOZ
Рис. 12
YOZ
Рис. 13
2.65 Расчет параметров валов
Опасным сечением по полученным эпюрам является сечение
![]() (22)
(22)
![]()
![]()
Вычислим приведенные моменты:
![]() (23)
(23)
![]()
![]()
зная, приведенный крутящий момент диаметр вала
 , (24)
, (24)
Вычислим :


Кноструктивно
![]()
![]()
Расчет диаметра штифта:
 (25)
(25)


Принимаем:
2.7 Выбор подшипников:
В данном проектируемом механизме будем использовать подшипники качения.
Выбирать будем, руководствуясь следующими параметрами:
Осевая сила
FА=0, следовательно, выбираем радиальный подшипник.Исходя из рассчитанных диаметров валов и справочных данных выберем подшипники для выходного и предвыходного валов. Радиальную силу действующую на подшипник определим как максимальную реакцию опоры:
![]()
![]()
Для выходного вала, выбираем подшипники типа 1000095 с размерами
d=5мм, D=13мм и динамической грузоподъемностью С=850Н.Расчетная долговечность в часах:
 (26)
(26)

Для предвыходного вала, выбираем подшипники типа 1000094 с размерами
d=4мм, D=11мм и динамической грузоподъемностью С=750Н.Расчетная долговечность в часах:

такая долговечность вполне согласуется с долговечностью работы приборных устройств.
Результаты выбора подшипников Таблица 9
|
Предвыходной вал |
Выходной вал |
||
|
Тип подшипника |
Долговечность, ч |
Тип подшипника |
Долговечность, ч |
|
Радиальный однорядный ГОСТ 8338-57 1000094 d=4 мм,D=11мм С=750Н |
|
Радиальный однорядный ГОСТ 8338-57 1000095 d=5 мм, D=13мм С=850Н |
|
2.8 Оценка уровня унификации конструкции
Одним из критериев качества изделия является коэффициент унификации или интегральный коэффициент. Эти коэффициенты дают возможность оценить уровень унификации и стандартизации изделия , т.е. оценить целесообразность конструкции исходя из ее экономичности.
Коэффициент унификации


Интегральный коэффициент
где
N –общее количество составных частей изделия в штукахN0-
общее количество оригинальных составных частей изделия в штукахn-
общее количество типоразмеров составных частей изделияn0-
общее количество типоразмеров оригинальных составных частей изделияИспользуя данные из спецификации вычислим эти коэффициенты для проектируемого прибора:
Таблица
10|
N |
N0 |
n |
n0 |
|
106 |
32 |
38 |
24 |


2.9
Рекомендации по сборке прибора.Прибор собирать в следующем порядке:
2.10 Расчет точности передачи
В Качестве показателей точности передачи принимаем кинематическую погрешность и мертвый ход,
определяемый только для реверсивных передач.При расчете точности применяют два метода: метод расчета на максимум - минимум и вероятностный метод.
Метод расчета на максимум - минимум основан на учете предельных отклонений и самых неблагоприятных их сочетаний . Метод гарантирует выполнение требований по точности передач.
Вероятностный метод расчета базируется на законах распределения погрешностей звеньев передач и вероятности различных их сочетаний, которая, в свою очередь, зависит от допустимого процента брака P. При практических расчетах коэффициент обычно принимают равным P=0.27.
После рас
2.10.1
Определение параметров передачи и выбор необходимых показателей точности.Определяется межосевое расстояние
 , (29)
, (29)
где
На примере первой передачи:
 .
.
Параметры зубчатых передач Таблица 11
|
Зубчатое колесо |
Число зубьев |
|
|
|
|
|
|
|
|
мкм |
|
|
|
|
20 |
12 |
18.9 |
22 |
1 |
8 |
14 |
21 |
38 |
16 |
0.75 |
0.96 |
|
|
43 |
25.8 |
27 |
23 |
38 |
20 |
||||||
|
|
18 |
10.8 |
27 |
22 |
9 |
18 |
21 |
38 |
16 |
0.9 |
||
|
|
72 |
43.2 |
30 |
26 |
58 |
22 |
||||||
|
|
18 |
10.8 |
32.4 |
22 |
11 |
20 |
21 |
38 |
16 |
0.87 |
||
|
|
90 |
54 |
35 |
30 |
58 |
26 |
||||||
|
|
18 |
10.8 |
32.4 |
22 |
11 |
20 |
21 |
38 |
16 |
0.87 |
||
|
|
90 |
54 |
35 |
30 |
58 |
26 |
Все зубчатые колеса имеют степень точности 7, вид сопряжения
G и модуль m=0.6мм.
![]()
![]() , (30)
, (30)
где
![]()
![]() , (31)
, (31)
где
![]() , (32)
, (32)
где
![]()
Рассчитаем минимальную кинематическую погрешность для первой передачи:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Переведем значение минимальной кинематической погрешности в угловые величины по формуле
 , (33)
, (33)
где

Аналогичным образом рассчитывается значение
![]()
![]() ,
,
где К – коэффициент, зависящий от передаточного отношения (см. табл. 11).
Выполним расчет для первой ступени:
![]() .
.
Переведем в угловые величины по формуле (34):
 [
[
![]()
 , (35)
, (35)
где
![]()
Найдем
 .
.
Переведем в угловую величину по формуле
 , (36)
, (36)
где
 .
.
![]()
![]() , (37)
, (37)
где
![]()
Найдем
![]() .
.
Переведем в угловую величину по формуле (37)
 .
.
Погрешность
![]() . (38)
. (38)
Для первой ступени:
![]()
Аналогично расчитывается
![]()
Таблица 12
|
Зубчатое колесо |
Передаточное отношение |
|
|
|
|
|
|
|
|
2.14 |
8.53 |
17.6 |
2.41 |
9.45 |
10.94 |
27.05 |
|
|
|||||||
|
|
4 |
7.31 |
11 |
1.62 |
13.87 |
8.93 |
24.87 |
|
|
|||||||
|
|
5 |
6.1 |
9.43 |
1.56 |
11.66 |
7.66 |
21.09 |
|
|
|||||||
|
|
5 |
6.1 |
9.43 |
1.56 |
11.66 |
7.66 |
21.09 |
|
|
Выберем коэффициент вероятности
Значения коэффициента вероятности Таблица 13
|
Зубчатое колесо |
Передаточное отношение |
|
|
|
2.14 |
0.81 |
|
|
||
|
|
4 |
0.88 |
|
|
||
|
|
5 |
0.94 |
|
|
||
|
|
5 |
0.94 |
|
|
Расчет кинематической погрешности вероятностным методом производится по формуле
![]() . (39)
. (39)
Для первой ступени:
Расчет погрешности мертвого хода вероятностным методом производится по формуле
![]() . (40)
. (40)
Для первой ступени:
Расчет суммарной средневероятностной погрешности проводится по формуле
![]() . (41)
. (41)
Для первой ступени:
Таблица 14
|
Зубчатое колесо |
|
|
|
|
|
14.256 |
7.65 |
16.17 |
|
|
|||
|
|
9.7 |
12.2 |
15.6 |
|
|
|||
|
|
8.86 |
11 |
14.1 |
|
|
|||
|
|
8.86 |
11 |
14.1 |
|
|
Расчет погрешности для редуктора проводится по формуле
 (42)
(42)
Вычислим это значение:

Полученное значение погрешности меньше максимально возможной заданной погрешности :
![]()
|
1. Техническое предложение |
4 |
|
2. Технический проект |
5 |
|
2.2 Разработка кинематической схемы |
6 |
|
2.3 Расчет ошибки передачи |
9 |
|
2.5 Расчет крутящих моментов |
11 |
|
2.5.1 Расчет размеров зубчатых колес |
12 |
|
2.6 Расчет валов |
14 |
|
2.7 Выбор подшипников: |
23 |
|
2.8 Оценка уровня унификации конструкции |
24 |
|
2.9 Рекомендации по сборке прибора. |
24 |
|
2.10 Расчет точности передачи |
25 |